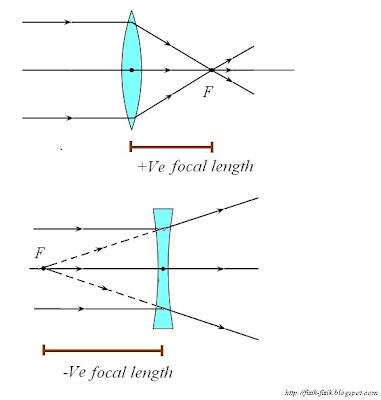
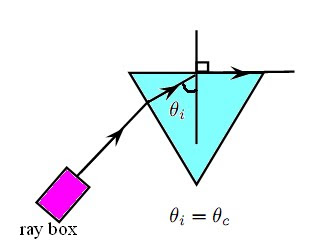
The angles of incidence and refraction when light travels from one medium to another can be calculated using Snell’s Law.
Definition: Snell’s Law
n1sin θ1 = n2 sin θ2where
n
1 = Refractive index of material 1
n
2 = Refractive index of material 2
θ
1 = Angle of incidence
θ
2 = Angle of refraction

If
n2 <>1then from Snell’s Law,
sin
θ1 < style="font-style: italic;">θ2.
For angles smaller than 90◦, sin
θ increases as
θ increases. Therefore,
θ1 < θ2.This means that the angle of incidence is less than the angle of refraction and the light ray is
away toward the normal.

Similarly,if
n2 > n1then from Snell’s Law,
sin θ1 > sin θ2.For angles smaller than 90◦, sin
θ increases as
θ increases. Therefore,
θ1 > θ2.This means that the angle of incidence is greater than the angle of refraction and the light ray is
bent toward the normal.What happens to a ray that lies along the normal line?Worked Example : Using Snell’s Law
Question:
A light ray with an angle of incidence of 35◦ passes from water to air.
Find the angle of refraction using Snell’s Law . Discuss the meaning of your answer.
(the refractive index is 1,333 for water and about 1 for air)
Answer
According to Snell’s Law: n1sin θ1 = n2 sin θ2 1.33 sin 35◦ = 1 sin θ2 sin θ2 = 0.763 θ2 = 49.7◦ The light ray passes from a medium of high refractive index to one of low refractive index. Therefore, the light ray is bent away from the normal.Test your understanding :
1. A light ray passes from water to diamond with an angle of incidence of 75◦. Calculate the angle of refraction. Discuss the meaning of your answer.
(Answer: 32.1◦, ....bent towards the normal)
 If the gap is bigger than the wavelength,
If the gap is bigger than the wavelength,